The results of diamond cut studies carried out in Moscow State University

A group of researchers from Moscow State University in collaboration with "LAL" company performed independent studies of diamond cut with the use of their own computer model. While maintaining the shape and pattern of the facets of a round diamond, they varied its cut parameters in order to find out those values providing the maximum light return and fire (colored rays of light arising due to the dispersion of the gem). Taking into account the conservatism of the diamond market, only the following cut parameters were considered in the studies reported: the table size (Dp) - 60% and 53% (the results obtained for diamonds having other values of Dp will be published later); the girdle thickness (in narrow part) (h) - 1%; the lower girdle facet size (q) - 82%. The light-diamond interaction was modeled for various types of light sources.

The main results of the light return and fire studies are summarized below

Macroanalysis

The pavilion angle ranged from 35° to 52°, the crown angle - from 15° to 45°. Among all the possible combinations of the parameters, there were a few parameter sets that maximized the light return and fire of the diamond. Some of the sets are currently used by manufacturers or coincide with those previously obtained by Tolkowsky and researchers from GIA. This argues for the validity of the proposed model. Other parameter sets that yield high coefficients of light return or fire are beyond conventional ranges (cut classes). The calculated fields with close light return coefficients have a complex shape with a pronounced diagonal orientation in the crown angle - pavilion angle coordinate system (see Fig.1).

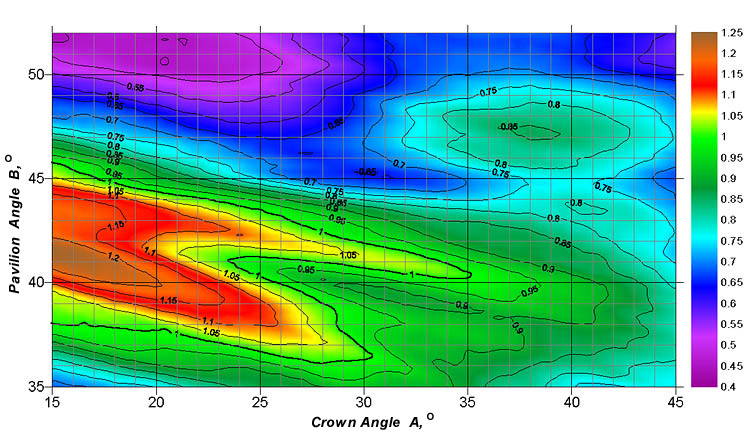
Figure 1. The light return coefficient nLR_30 for a diamond with the table size Dp=53%. The illumination: diffused (a source of diffused daylight of the "Office" type).

The relationship between the fire strength and the crown and pavilion angles is even more complex. It strongly depends on the illumination conditions.

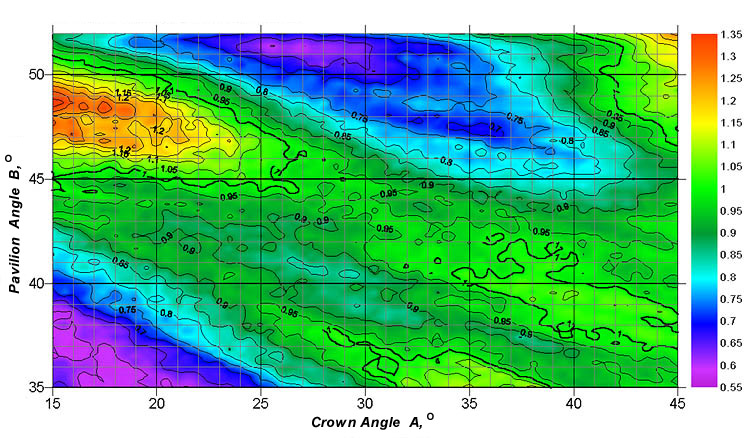
Figure 2. The fire coefficient nMF_30 for a diamond with the table size Dp=53%.

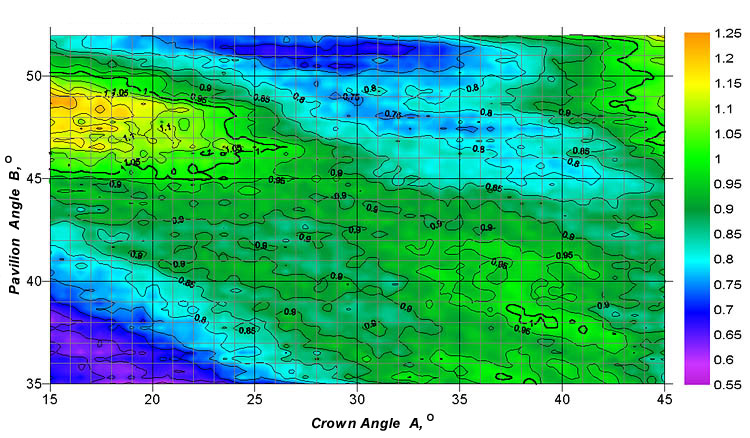
Figure 3. The fire coefficient nMF_30 for a diamond with the table size Dp=60%.

Photorealistic images of Tolkowsky diamond, a diamond with high light return and a diamond showing strong fire but weak light return. The light sources model "Office" illumination conditions.

Diamond by Tolkowsky	Diamond with high light return	Diamond showing strong fire
A = 34.5° B= 40.75° Dp= 53% Gd=2.7%	A = 20° B= 40° Dp= 53% Gd=2.3%	A = 15° B= 48.5° Dp= 53% Gd=2.4%

Photorealistic images of the same diamonds but illumination conditions model those actually used for taking photographs of diamonds (a few lateral sources of diffused light).

Diamond by Tolkowsky	Diamond with high light return	Diamond showing strong fire
A = 34.5° B= 40.75° Dp= 53% Gd=2.7%	A = 20° B= 40° Dp= 53% Gd=2.3%	A = 15° B= 48.5° Dp= 53% Gd=2.4%

Мicroanalysis

The pavilion angle ranged from 38° to 43°, the crown angle - from 30° to 40°. In different grading systems, the existing cut classes look like rectangular parallelepipeds.

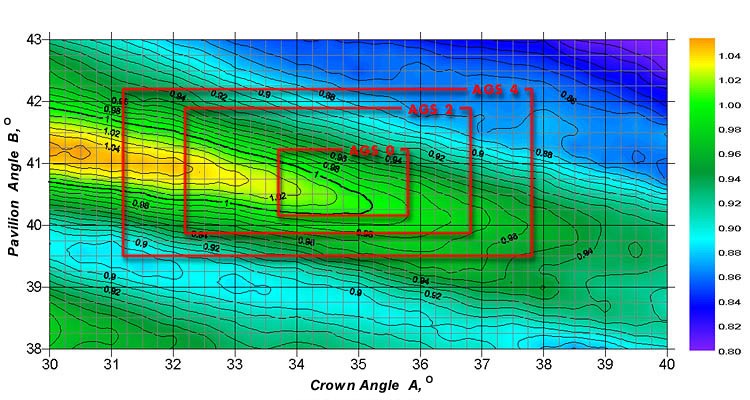
Figure 4. The light return coefficient nLR_30 for a diamond with the table size Dp=53%. The illumination: diffused (a source of diffused daylight of the "Office" type).

Within these parallelepipeds described in the grading systems, such as AGS, the light return and fire coefficients considerably vary. For example, some parameter sets belonging to group 3 may yield better light return and fire than some sets from group 0. This is true for all the existing cut grading systems that define the cut parameter groups as the rectangular parallelepipeds embedded in one another (see Fig.4-6).

Figure 5. The fire coefficient nMF_30 for a diamond with the table size Dp=53%.

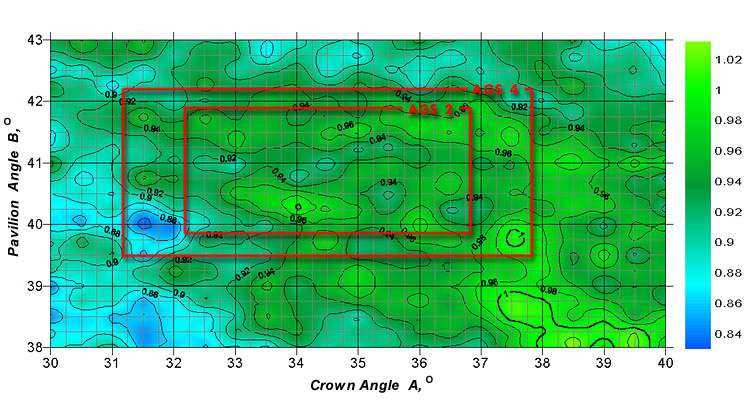
Figure 6. The fire coefficient nMF_30 for a diamond with the table size Dp=60%.

Photorealistic images of diamonds have cut parameters on the cut grade AGS 2 borderline. The left image is diamond with minimum and the right image is diamond with maximum light return for all cut grade AGS 2. The light sources model "Office" illumination conditions.

A = 32.2° B = 40.9° Dp=53% Gd=2.6%	A = 32.2° B = 41.3° Dp=53% Gd=2.6%	A = 36.8° B = 40.25° Dp=53% Gd=2.7%	A = 36.8° B = 41.86° Dp=53% Gd=2.8%
nLR_30=1.05 nMF_30=1.00	nLR_30=1.02 nMF_30=0.98	nLR_30=0.97 nMF_30=1.00	nLR_30=0.86 nMF_30=1.0

Photorealistic images of the same diamonds but illumination conditions model those actually used for taking photographs of diamonds (a few lateral sources of diffused light).

A = 32.2° B = 40.9° Dp=53% Gd=2.6%	A = 32.2° B = 41.3° Dp=53% Gd=2.6%	A = 36.8° B = 40.25° Dp=53% Gd=2.7%	A = 36.8° B = 41.86° Dp=53% Gd=2.8%
Q=1.05 EFF=1.07	Q=1.00 EFF=0.98	Q=0.97 EFF=0.97	Q=0.86 EFF=0.79

The cut parameters yielding high values of the light return.

The proposed model shows better light return and fire for the solutions proposed by Tolkowsky.

Optimizing the cut parameters of a diamond solely with respect to its light return (the authors think that this is insufficient in principle) provides some zones with a light return coefficient value considerably exceeding Tolkowsky's values and those of other ideal diamond cuts. One of such zones corresponds to small values of the crown angle.

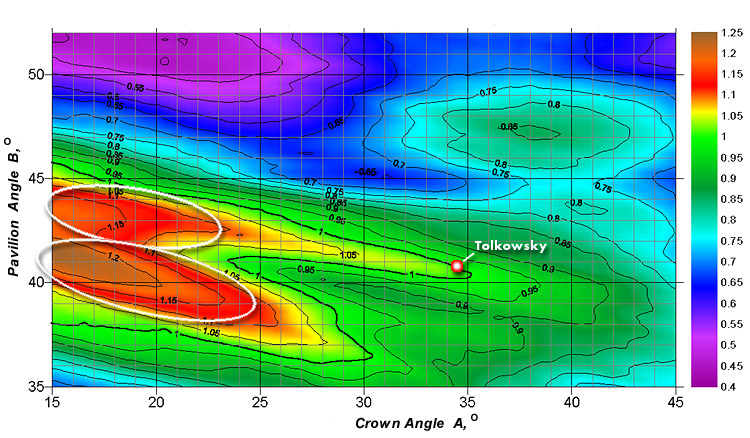
Figure 1b. The point corresponding to Tolkowsky cut and the zones of maximum light return on the plot of the light return coefficient nLR_30 for a diamond with the table size Dp=53%.

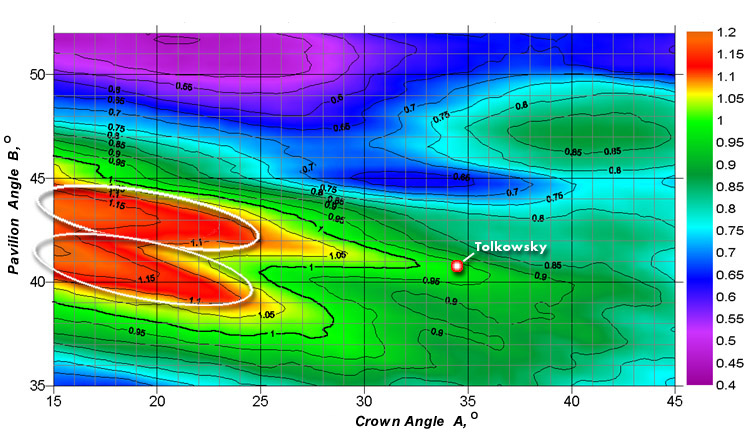
Figure 20b. The projection of Tolkowsky cut and the zones of maximum light return on the plot of the light return coefficient nLR_30 for a diamond with the table size Dp=60%.

The same result has been noticed by the GIA group. The authors of the present work propose to compare the future results of diamond cut studies using the light return, fire, and other important coefficients and normalizing them so that for the Tolkowsky cut all they are equal to unity.

Photorealistic images of Tolkowsky diamond, and diamonds with higher light return but uncommon brilliance pattern. The light sources model "Office" illumination conditions

nLR_30 = 1 nMF_30 = 1	nLR_30 = 1.23 nMF_30 = 0.81	nLR_30 = 1.17 nMF_30 = 0.96
A = 34.5° B= 40.75° Dp= 53% Gd=2.7%	A = 16° B= 41° Dp= 53% Gd=2.2%	A = 18° B= 43° Dp= 53% Gd=2.3%

Photorealistic images of the same diamonds but illumination conditions model those actually used for taking photographs of diamonds (a few lateral sources of diffused light).

Q = 1.00 EFF = 1.00	Q = 1.00 EFF = 0.78	Q = 1.12 EFF = 1.05
A = 34.5° B= 40.75° Dp= 53% Gd=2.7%	A = 16° B= 41° Dp= 53% Gd=2.2%	A = 18° B= 43° Dp= 53% Gd=2.3%

The cut quality function Q.

In general, the ranges of the cut parameters yielding high values of the light return coefficient do not coincide with those ranges optimizing the fire. In other words, it is almost impossible to maximize the fire without sacrificing the total light return in the direction of the observer. Since none of these characteristics of a diamond can be considered as paramount, the authors propose a special function that characterizes the cut parameters from the point of view of the light return and fire simultaneously (Fig.7-8).

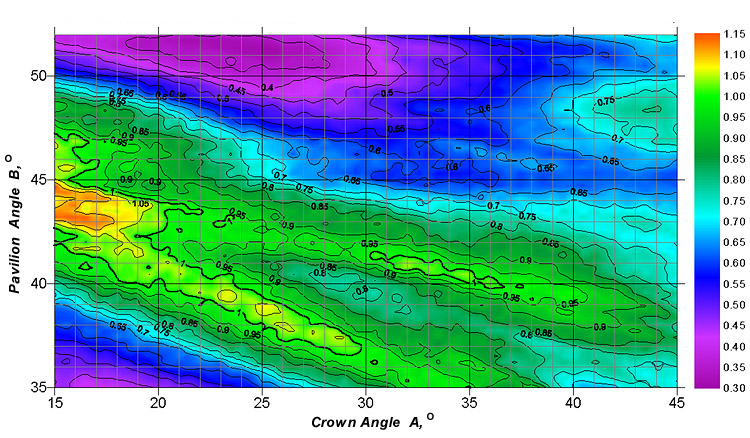
Figure 7. The distribution of the cut quality function Q (Macroanalysis) for a diamond with the table size Dp=53%

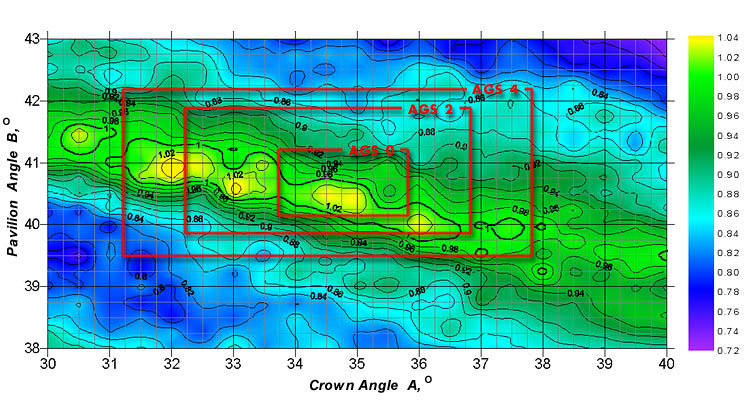
Figure 8. The distribution of the cut quality function Q (Microanalysis) for a diamond with the table size Dp=53%

Photorealistic images of diamonds belonging to different AGS cut grades but having cut quality coefficient Q close to maximum. The light sources model "Office" illumination conditions.

AGS 4 nLR_30=1.05 nMF_30=1.00	AGS 0 nLR_30=1.00 nMF_30=1.04	AGS 0 nLR_30=0.92 nMF_30=0.96	AGS 2 nLR_30=0.99 nMF_30=1.05
A = 32° B = 41° Dp=53% Gd=2.6%	A = 34.75° B = 40.4° Dp=53% Gd=2.7%	A = 35.8° B = 41.25° Dp=53% Gd=2.7%	A = 36° B = 40° Dp=53% Gd=2.7%

Photorealistic images of the same diamonds but illumination conditions model those actually used for taking photographs of diamonds (a few lateral sources of diffused light).

AGS 4 Q=1.05 EFF=1.07	AGS 0 Q=1.04 EFF=1.09	AGS 0 Q=0.88 EFF=0.80	AGS 2 Q=1.04 EFF=1.09
A = 32° B = 41° Dp=53% Gd=2.6%	A = 34.75° B = 40.4° Dp=53% Gd=2.7%	A = 35.8° B = 41.25° Dp=53% Gd=2.7%	A = 36° B = 40° Dp=53% Gd=2.7%

The cut efficiency function EFF

The cut parameters of a diamond affect material losses that appear as a result of cutting the diamond. If changing the parameters improves the appearance of the cut diamond but decreases its weight, additional analysis is required to compare the two effects. Such analysis can determine those zones in which either an increase in the light return and fire does not considerably reduce the weight or an increase in the weight does not lead to considerable reduction of the light return and fire. In this connection, it is important to take into account various ways of marking a rough diamond as well as traditional requirements for diamond geometry that exist on the market. Additional investigations are needed to find out how the price of a diamond exactly depends on both its weight and appearance.

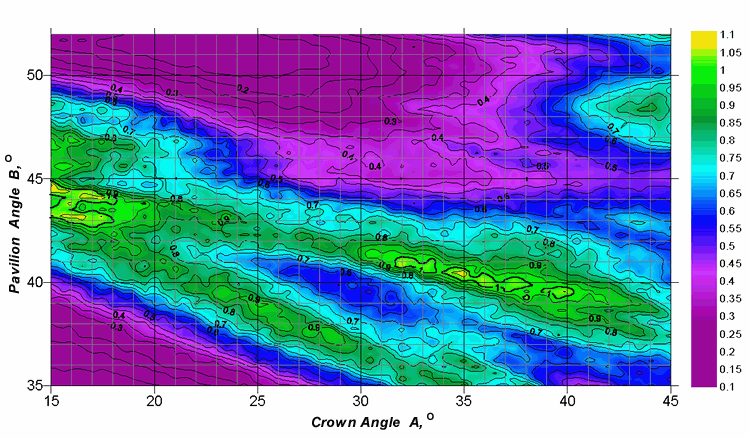
Figure 9. The distribution of the cut efficiency function EFF for a diamond with the table size Dp=53%.

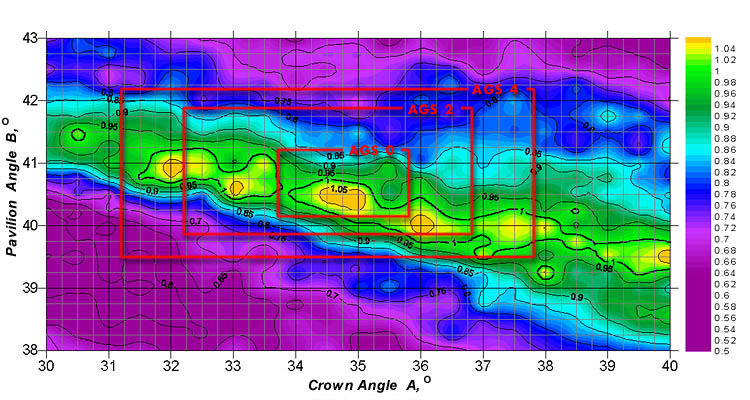
Figure 10. The distribution of the cut efficiency function EFF for a diamond with the table size Dp=53%.

The results of the reported studies can be used as practical recommendations for cutting diamonds

To cut a diamond, a manufacturer can use parameter zones that yield a high light return coefficient and strong dispersion at the same time. It is up to the manufacturer whether the cut diamond will show worse light return but better fire or vice versa. For this purpose, the crown angle of the diamond should be changed according to the changes in its pavilion angle.

Photorealistic images of Tolkowsky diamond, a diamond with high light return and a diamond showing strong fire. The light sources model combined illumination conditions "Office" + "Chandelier"

Diamond by Tolkowsky	Diamond with high light return	Diamond showing strong fire
A = 34.5° B= 40.75° Dp= 53% Gd=2.7%	A = 25° B= 42.3° Dp= 53% Gd=2.4%	A = 39.9° B= 39.6° Dp= 57% Gd=2.8%

The colored diamonds optimization

By analyzing the cut parameters with taking into account the color of the modeled diamond, it is possible to obtain some results useful for cutting colored diamonds.

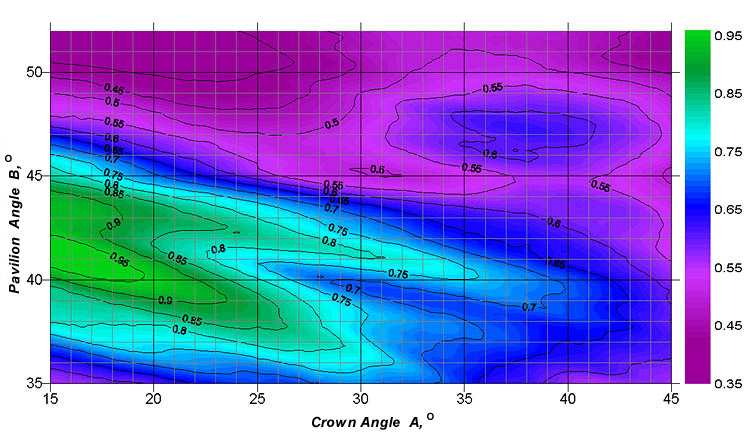
Figure 11. The light return coefficient nLR_30 for a yellow diamond (the absorption spectrum typical for a diamond of the "Cape" series) with the table size Dp=53%. The illumination: diffused (a source of diffused daylight of the "Office" type).

Due to their coloration, most such gems show almost no fire. So, only the light return should be optimized for them. There are two different cut solutions that yield a high light return coefficient.

Photorealistic images of yellow diamonds

common brilliance pattern	uncommon brilliance pattern with higher light return
A = 34° B = 41° Dp=60% Gd=3.7%	A = 25° B = 39° Dp=60% Gd=3.4%

They essentially differ in the brilliance pattern. [Details].Unfortunately, the solution with the better brilliance pattern yields a smaller weight (for diamonds of equal diameters). On the other hand, these cut parameters are practical for flat crystals or in the case when a rough crystal should be cut symmetrically (then, the total yield increases due to the crown flatness).

Diamond modeling software

When varying the proportions and angles of a diamond, one may get a sample with a pattern unacceptable for today's traditional market (such as "Fish Eye" or "Nail Head" effects), even if the light return and fire of the diamond are perfect. Therefore, it is reasonable to view a virtual 3D image of such an uncommon gem. We offer those visitors of our web-site who use the Internet Explorer browser to play with a demo of "Brill" software, the one used for modeling the diamond and calculating its light return and fire. When changing the cut parameters of the diamond and its orientation, you can see online the photorealistic image of the gem. Also you can vary the point and angle of incidence of a light ray that falls onto the diamond and trace the ray with taking into account its refraction and reflections (including Fresnel losses).