The "Diamond Design" by Tolkowsky. A Study of the Reflection and Refraction of Light in Diamond

Table of Contents
Back of the Brilliant
Let us now pass to the consideration of the other alternative, i.e. where the top surface is a horizontal plane AB and where the bottom surface AC is inclined at an angle (to the horizontal (fig. 25)). As before, we have to introduce a third plane BC to have a symmetrical section.
First Reflection
Let a vertical ray PQ strike AB. As the angle of incidence is zero, it passes into the stone without refraction and meets plane AC at R. Let RN be the normal at that point, then, for total reflection to occur, angle NRQ = 24°26'. But, angle NRQ = angle QAR - a as AQ and QR, AR and RN are perpendicular.
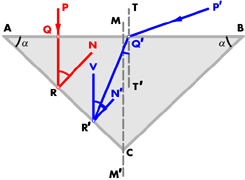 Fig. 25
Fig. 25
Therefore, for total reflection of a vertical ray, a = 24°26'. Let us now incline the ray PQ so that it gradually changes from a vertical to a horizontal direction, and let P'Q' be such a ray. Upon passing into the diamond it is refracted, and strikes AC at an angle Q'R'N' where R'N' is the normal to AC. When P'Q' becomes horizontal, the angle of refraction T'Q'R' becomes equal to 24°26'. This is the extreme value attainable by that angle; also, for total reflection, angle Q'R'N' must not be less than 24°26'. If we draw R'V, vertical angle VR'Q' = R'Q'T' = 24°26', and angle VR'N' = VR'Q' + Q'R'N' =24°26' + 24°26' = 48°52' as before, a = angle VR'N', and therefore a = 48°52 (9).
For absolute total reflection to occur at the first facet, the inclined facets must make an angle of not less that 48°52' with the horizontal.
Second Reflection
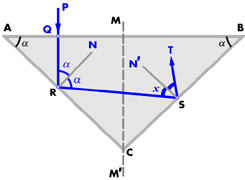 Fig. 26
Fig. 26
When the tray of light is reflected from the first inclined facet AC (fig. 26), it strikes the opposite one BC. Here too the light must be totally reflected, for otherwise there would be a leakage of light through the back of gem stone. Let us consider, in the first instance, a ray of light vertically incident upon the stone. The path of the ray will be PQRST. If RN and SN' are the normals at R and S respectively, then for total reflection, angle N'SR = 24°26'. Let us find the value of a to fulfil that condition: angle QRN = angle QAR = a as having perpendicular sides. angle SRN = angle QRN as angles of incidence and reflection. Therefore angle NRS = a. Now let angle N'SR = c. Then, in triangle RSC,
angle SRC = 90° - a
angle RSC = 90° - c
angle RCS = 2 x angle RCM = 2 x ARQ = 2 (90° - a).
The sum of these three angles equals two right angles,
90° - a + 90° - c + 180° - 2a = 180°, or
3a+ c = 180° 3a = 180° - c.
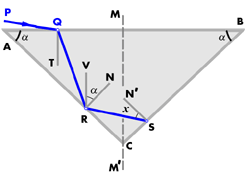 Fig. 27
Fig. 27
Now, c is not less than 24°26', therefore a is not greater than a = (180 - 24°26')/3 = 51°51'. Let us again incline PQ from the vertical until it becomes horizontal, but in this case in the other direction, to obtain the inferior limit. Then (fig.27) the path will be PQRS. Let QT, RN, SN' be the normals at Q, R, and S respectively. At the extreme case, TQR will be 24°26'. Draw RV vertical at R.
Then angle QRV = angle TQR = 24°26' angle VRN = a.
As before, in triangle RSC,
angle SRC = 90° - NRS = 90° - a - 24°26'
angle RCS = 2 a (90° - a)
angle RSC = 90° - c.
Then
90 - a - 24°26' + 180° - 2a + 90° - c = 180°
3a + x = 180° - 24°26' = 155°34'
3a = 155°34' - c.
In the case now considered,
c = 24°26'.
Then
3a = 155°34' - 24°26' = 131° 8'
a = 43°43' (10)
For absolute total reflection at the second facet, the inclined facets must make an angle of not more than 43°43' with the horizontal.
We will note here that this condition and the one arrived at on "First Reflection" are in opposition. We will discuss this later, and will pass now to considerations of refraction.
Refraction. First case: a is a less than 45°
In the discussion of refraction in a diamond, we have to consider two cases, i.e. a is less than 45° or it is more than 45°. Let us take the former case first and let PQRST (fig. 28)
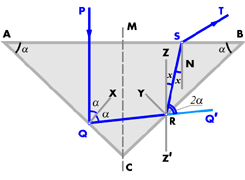
Fig. 28
be path of the ray. Then, if SN is the normal at S, we know that for total reflection at S angle RSN = 24°26'. We want to avoid total reflection, for if the light is thrown back into the stone, some of it may be lost, and in any case the ray will be broken too frequently and the result will be disagreeable. Therefore, angle RSN = 24°26' (11). Suppose this condition is fulfilled and the light leaves the stone along ST. It is refracted, and its colors are dispersed into a spectrum. It is desirable to have this spectrum as long as possible, so as to disperse the various colors far away from each other. As we know, this will give us the best possible "fire" This result will be obtained when the ray is refracted thought the maximum angle. By (11) the value for that angle is 24°26', and (11) becomes angle RSN = 24°26' for maximum dispersion.
But then the light leaves AB tangentially, and the amount of light passing is zero. To increase that amount, the angle of refraction has to be reduced. The angle of dispersion decreases simultaneously, but the amount of light dispersed increases much more rapidly. Now we know that the angle of dispersion is proportional to the sine of the angle of refraction. It is, moreover, proved in optics that the amount of light passing through a surface as at AB is proportional to the cosine of the angle of refraction. The brilliancy produced is proportional both to the amount of light and to the angle of dispersion, and therefore to their product, and (by the theory of maxima and minima) will be maximum when they are equal, i.e. when the sine and cosine of the angle of refraction are equal. For maximum brilliancy, therefore, the angle of refraction should be 45°. This gives for angle RSN
sin RSN = sin 45°/ 2.417 = 0.7071 / 2.417 = 0.2930
therefore, angle RSN = 17° for optimum brilliancy (12).
Let (fig.28) QX and RY be the normals at Q and R respectively, and ley ZZ' be vertical through R. We know that angle RQX = angle PQX = a, therefore angle PQR = 2a.
Produce QR to Q'. Then, as PQ and ZZ' are parallel,
angle ZRQ' = angle PQR = 2a.
Now, let angle RSN = c (= 17° for optimum brilliancy). Then, as ZZ' and SN are parallel, angle ZRS = c. As they are complements to angles of incidence,
angle QRC = angle SRB = i (say),
but
angle Q'RB = angle QRC,
therefore
angle SRQ' = 2i.
In angle ZRQ' we have
angle ZRQ' = angle ZRS + angle SRQ'
2a = c + 2i. (13)
In triangle QCR
angle RCQ = 90° - a
angle QRC = i
angle QCR = 2 (90° - a),
therefore
(90° - a) + i + 180° - 2a = 180°,
i = 3a - 90°.
Introduce this value of i in (13), 2a = c + 6a - 180°
4a = 180° - c
and giving x its value 17°, 4a= 180° - 17° = 163°
a = 40°45' (14).
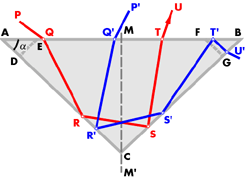
Fig. 29
If we adopt this value for a, the paths of oblique rays will be as shown in fig. 29, PQRST when incident from the left of the figure, and P'Q'R'S'T' when incident from the right. Ray PQRST will leave the diamond after the second reflection, but with a smaller refraction than that of a vertically incident ray, and therefore with less "fire". Oblique rays incident from the left are, however, small in number owing to the acute angle QRA with which they strike AC; the loss of fire may therefore be neglected. Ray P'Q'R'S'T' will strike AB at a greater angle of incidence than 24°26', and will be reflected back into the stone.
This is a fault that can be corrected by the introduction of inclined facets DE, FG; ray P'Q'R'S'T'' will then strike FG at an angle less than 24°26', and this angle can be arranged by suitably inclining FG to the horizontal so as to give the best possible refraction. The amelioration obtained by thus taking full advantage of the refraction is so great that the small loss of light caused by that arrangement of the facets is insignificant : the leakage occurs through the facet CB, near C, where the introduction of the facet DE allows light to reach CB at an angle less than the critical. In a brilliant, where CB is the section of the triangular side of an eight-sided pyramid, the area near the apex C is very small, and the leakage may therefore be considered negligible.
Refraction. Second case: a is a greater 45°
In this case the path of a vertical ray will be as shown by PQRST in fig. 30, and the optimum value for a,
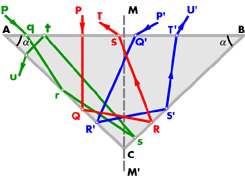
Fig. 30
which may be calculated as before, will be a = 49°13'.(15) As regards the vertical rays, this value gives a fire just as satisfactory as (14) a = 40°45'; let us consider what happens to oblique rays. Rays incident from the left as pqrstu may strike BC at an angle of incidence less than the critical, and will then leak out backwards. Or they may be reflected along st , and may then be reflected into the stone.
Both alternatives are undesirable, but they do not greatly affect the brilliancy of the gem, because, as we have seen, the amount of light incident from the left is small. That incident from the right is, on the contrary, large.
Let us follow ray P'Q'R'S'T'. It will be reflected twice, and will leave the diamond after the second reflection, like the vertically incident ray, but with a smaller refraction, and consequentially less fire; most of the light will be striking the face AB nearly vertically when leaving the stone, and the fire will be very small. This time it is impossible to correct the defect by introducing accessory facets, as the paths S'T' of the various oblique rays are not localized near the edge B, but are spread over the whole of the face; we are therefore forced to abandon this design.
Summary of the results obtained for a
We have found that:
- For first reflection, a must be greater than 48°52'.
- For second reflection, a must be less than 43°43'.
- For refraction, a may be less or more than 45°. When more, the best value is 49°15', but it is unsatisfactory. When less, the best value is 40°45', and is very satisfactory, as the light can be arranged to leave with the best possible dispersion.
Upon consideration of the above results, we conclude that the correct value for a is 40°45', and gives the most vivid fire and the greatest brilliancy, and that although a greater angle would give better reflection, this would not compensate for the loss due to the corresponding reduction in dispersion. In all future work upon the modern brilliant we will therefore take a = 40°45'.
Front of the Brilliant
When arriving at the value of a = 40°45', we have explained how the use of that angle introduced defects which could be corrected by the use of extra facets. The section will therefore be shaped somewhat as in fig.31. It will be convenient to give to the different facets the names by which they are known in the diamond cutting industry.
These are as follows:
- AC and AB are called pavilions or quoins (according to their position relative to the axis of crystallization of the diamond).
- AD and EB are similarly called bezels or quoins.
- DE is the table.
- FG is the culet, which is made very small and whose only purpose is to avoid a sharp point.
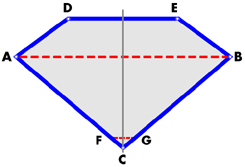
Fig. 31
Through A and B passes the girdle of the stone. We have to find the proportions and inclination of the bezels and the table. These are best found graphically. We know that the introduction of the bezels is due to the oblique rays; it is therefore necessary to study the distribution of these rays about the table, and to find what proportion of them is incident in any particular direction.
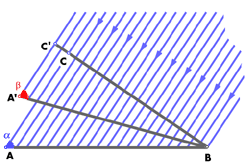
Fig. 32
Consider a surface AB (fig.32) upon which a beam of light falls at an angle a. Let us rotate the beam so that the angle becomes a (for convenience, the figure shows the surface AB rotated instead to A'B, but the effect is the same). The light falling upon AB can be stopped in the first case by intercepting it with screen BC, and in the second with a screen BC' where BCC' is at right angles to the direction of the beam. And if the intensity of the light is uniform, the length of BC and BC' will be a measure of the amount of light falling upon AB and AB' respectively.
Now
BC = AB sin a
BC' = A'B sin b - AB sin b.
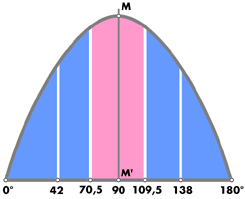
Fig. 33
Therefore, other things being equal, the amount of light falling upon a surface is a proportional to the sine of the angle between the surface and the direction of the light. We can put it as follows: If uniformly distributed light is falling from various directions upon a surface AB, the amount of light striking it from any particular direction will be proportional to the sine of the angle between the surface and that direction. If we draw a curve between the amount of light striking a surface from any particular direction, and the angle between the surface and that direction, the curve is equally distributed and of equal intensity in all directions. For calculations we can assume this to be the case, and we will take the distribution of the quantity of light at different angles to follow a sine law.
It is convenient to divide all the light entering a diamond into three groups, one of vertical rays and two of oblique rays, such that the amount of light entering from each group is the same.
Now in the sine curve (fig.33) the horizontal distances are proportional to the angles between the table of a diamond and the direction of the entering rays; the vertical distances are proportional to the amount of light entering at these angles. The total amount of light entering will be proportional to the area shaded. That area must therefore be divided into three equal parts; this may be done by integrals, or by drawing the curve on squared paper, counting the squares, and drawing two vertical lines on the paper so that one-third of the number of the squares is on either side of each line.
By integrals,
area = integral [sin c dx] = - cos c.
total area = [- cos c] (for c=0 and c=180) = 1 + 1 = 2,
therefore
1/3 area = 2/3.
The value of a corresponding to the vertical dividing lines on the curve is thus given by
cos c = 1 - 2/3 = 1/3
cos c = 1 - 4/3 = - 1/3,
therefore c = 70.5° approximately and c = 109.5°.
Taking the value c = 90° as zero for reckoning the angles of incidence,
i = 90° - 70.5° = 19.5°
and i = 90° - 109.5° = - 19.5°.
The corresponding angles of refraction are
sin r = sin i / n = sin 19.5°/ 2.417 = 0.3333 / 2.417 = 0.1377
r = 7°52'.
The range of the different classes is thus as follows:
Angle of incidence :
vertical rays - 19.5° to + 19.5°
oblique rays - 90° to -19.5°
and +19.5° to +90°.
Angle of refraction.
vertical rays - 7°52' to + 7°52'
oblique rays - 24°26' to - 7°52'
and + 7°52' to + 24°26'.
The average angle of each of these classes may be obtained by dividing each of the corresponding parts on the sine curve in two equal parts. The results are as follows:
Angle of incidence:
vertical rays 0°
oblique rays - 16°
and + 16°.
For the design of the table and bezels, we have to know the directions and positions of the rays leaving the stone. The values just obtained would enable us to do so if all the rays entering the front of the gem also left there. We have, however, adopted a value for a (a = 40°45') which we know permits leakage, and we have to take that leakage into consideration.
The angle where leakage begins is inclined at 24°26' to the pavilion [fig.25]. We have thus
Q'R'N' = 24°26',
therefore
Q'R'A' = 90° - 24°26' - 65°34'.
Now in triangle AQ'R'
Q'R'A + AQ'R' + R'AQ' = 180°,
therefore
AQ'R' = 180° - 65°34' - 40°45' = 73°41'.
The limiting angle of refraction R'Q'T is thus
= 90° - 73°41' = 16°19',
corresponding to an angle of incidence of
sin i = n sin r = 2.417 sin 16°19' = 2.417 * 0.281 = 0.678. i = 42,5°
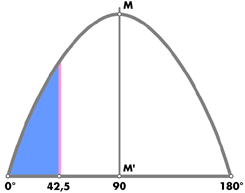
Fig. 34
Upon referring to the sine curve, we find that the area shaded (fig.34), which represents the amount of light lost by leakage, although not so large as if the same number of degrees leakage had occurred at the middle part of the curve, is still very appreciable, forming as it does about one sixth of the total area. Just under one-half (exactly 0.493) of the light incident obliquely from the right [fig.25] is effective, the other half being lost by leakage. Still, the sacrifice is worth while, as it produces the best possible fire. The oblique rays incident from the right range therefore 19.5° to 42.5°, with an average (obtained as before) of 30°15'. The corresponding refracted rays are 7°52', 16°19', and 12°0'. We have now all the information necessary for the design of the table and bezels.
Design of Table and Bezels
Let us start with the fundamental section ABC symmetrical about MM', making the angles ACB and ABC 40°45' (fig 35).
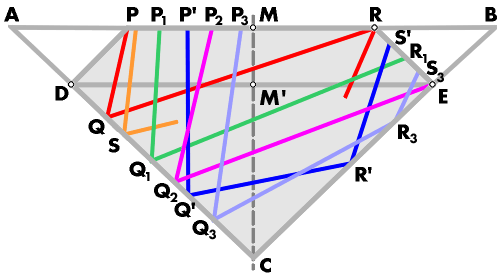
Fig. 35
The bezels have been introduced into the design to disperse the rays which were originally incident from the right upon the facet AB. To find the limits of the table, we have therefore to consider the path of limiting oblique ray. We know that this ray has an angle of incidence of 42,5° and an angle of refraction of 16°19'. Let us draw such a ray PQ : it will be totally reflected along QR, if we make PQN = NQR, where QN is the normal. Now QR should meet a bezel.
If the ray PQR was drawn such that MP = MR, then P and R will be the points at which the bezels should meet the table. For if PQ be drawn nearer to the center of the stone, QR will then meet the bezel, and if PQ be drawn further away, it will meet the opposite bezel upon its entry into the stone and will be deflected.
The first point to strike us is that no oblique rays incident from the left upon the table strike the pavilion AB, owing to the fact that the table stops at P. We will, therefore, treat them as non-existent, and confine our attention to the vertical rays and those incident from the right.
Let us draw the limiting average rays of these two groups, i.e. the rays of the average refractions 0° and 12° passing through P, PS, and PT. The length of the pavilion upon which the rays of these two groups fall are thus respectively CS and CT.
The rays of the first group P'Q'R'S' are all reflected twice before passing out of the stone, and make, after the second reflection, an angle of 17° with the vertical (as by eq.(12)). Of the rays of the second group, most are reflected once only (P1Q1R1) and make then an angle of 69,5° with the vertical (this angle may be found by measurement or by calculation). Part of the second group is reflected twice (P3Q3R3S3), and strikes the bezel at 29° to the vertical. This last part will be considered later, and may be neglected for the moment.
We have to determine the relation between the amount of light of the first group and of the first part of the second group. Now we know that the amount of oblique light reflected from a surface on pavilion AC is 0.493 of the amount of vertical light reflected (cp. [fig.34] and context). If we take as limit for the once reflected oblique ray the point E (as a trial) on pavilion BC, i.e. if it is at E that the girdle is situated, then the corresponding point of reflection for that oblique ray will be Q2 [fig.35]. The surface of pavilion upon which the oblique rays then act will be limited by S and Q2, and as in a brilliant the face AC is triangular, the surface will be proportional to SC2 Q2C2.
Similarly, the surface upon which the vertical group falls will be proportional to TC2.
Thus we have as relative amounts of light
for vertical rays: TC2
oblique rays: 0.493 (SC2 - QC2)
The first group strikes the bezel at 17° to the vertical, and the second at 69.5° to the vertical. The average inclination to the vertical will thus be
[ 17 x TC2 + 69.5 x 0.493 (SC2 - QC2) ] / [ TC2 + 0.493 (SC2 + 0.493 (SC2 - QC2) ]
Let us draw a line in that direction (through R, say), and let us draw a perpendicular to it through R, RE; then that perpendicular will be the best direction for the bezel, as a facet in that direction takes the best possible advantage of both groups of rays.
If the point E originally selected was not correct, then the perpendicular through R will not pass through E, and the position of E has to be corrected and the corresponding value of CQ2 correspondingly altered until the correct position of E is obtained.
For that position of E (shown on [fig.35]), measured scaled off the drawing give
CS = 2.67 CS2 = 7.12
CT = 2.13 CT2 = 4.54
CQ2 = 1.60 CQ22 = 2.56
CS2 - CQ2 = 4.57
Therefore the average resultant inclination will be
[ 17 * CT2 + 69.5 x 0.493 (CS2 - CQ2) ] / [ (CT2 + 0.493 (CS2 - CQ2) ] =
= [ 17 x 4.54 + 69.5 x 0.493 x 4.57 ] / [ 4.54 + 0.493 x 4.57 ] =
= [ 77.2 + 156.2 ] / [ 4.54 + 2.24 ] = 233.4 / 6.78 = 34.45 = 34,5°
to the vertical.
By the construction, the angle a, i.e. the angle between the bezel and the horizontal, has the same value
a = 34.5°.
The small proportion of oblique rays which are reflected twice meet the bezel near its edge, striking it nearly normally : they make an angle of 29° with the vertical. Facets more steeply inclined to the horizontal than the bezel should therefore be provided there. The best angle for refraction would be 29° + 17° = 46°, but if such an angle were adopted most of the light would leave in a backward direction, which is not desirable. It is therefore advisable to adopt a somewhat smaller value; an angle of about 42° is best.
Best Proportions of a Brilliant
We have thus as best section of a brilliant one as given in [fig.35], ABCDE, where
a = 40°45'
b = 34°30'.
DE is obtained from PR in [fig.35].
If we make the diameter AB of the stone100 units, then the main dimensions are in the following proportions [fig.35] :
|
Diameter AB = 100
|
Thickness above girdle MM' = 16.2
|
|
Table DE = 53
|
Thickness below girdle M'C = 43.1
|
|
Total thickness MC = 59.3
|
|
Fig.36 shows the outline of a brilliant with these proportions. These proportions can be approximated as follows:

Fig. 36
Fig. 37
In a well-cut brilliant the diameter of the table is one-half of the total diameter, and the thickness is six-tenths of the total diameter, rather more than one-quarter of the thickness being above the girdle and rather less than three-quaters below. It is to be noted here that a different proportions is generally for the thickness above the girdle ("one third of the total thickness"), both is works upon diamonds and by diamond polishers themselves. It is true that diamonds were cut thicker above the girdle and with a smaller table before the introduction of sawing, for then the table was obtained by grinding away a corner or an edge of the stone, and the loss in weight was thus considerable, and would have been very much greater still if the calculated proportions had been adopted. With the use of the saw, the loss in weight was enormously reduced and the manufacture of sawn stones became therefore much finer and more in accordance with the results given above. It is a remarkable illustration of conservatism that although diamonds have been cut for decades with 1/4 (approximately) of the thickness above girdle, yet even now the rule is generally stated as 1/3 of the thickness. Stones are still cut according to that rule, but then they are not sawn stones as a rule, and the thickness is left greater to diminish the loss in weight. The brilliancy is not greatly diminished by making the stone slightly thicker over the girdle.
Comparison of the Theoretically Best Values with those used in Practice
In the course of his connection with the diamond-cutting industry the author has controlled and assisted in the control of the manufacture of some million pounds worth diamonds which were all cut regardless of loss of weight, the only aim being to obtain the liveliest fire and the greatest brilliancy.
The most brilliant larger stones were measured and their measures noted. It is interesting to note how remarkably close these measures, which are based upon empirical amelioration and rule-of-thumb correction, come to the calculated values.
As an instance the following measures, chosen at random, are given (the dimensions are in millimeters):
| a | 40.75° | 40.75° | 40° | 41° | 41° |
| b | 35° | 35° | 34.5° | 33° | 34° |
| AB | 7.00 | 7.08 | 6.50 | 21.07 | 9.12 |
| MC | 4.12 | 4.35 | 3.61 | 12.34 | 5.47 |
| MM' | 1.08 | 1.32 | 0.85 | 3.31 | 1.61 |
These measures, worked out in percentage of AB, give:
| a | 40.75° | 40.75° | 40° | 41° |
41° |
40°42' | 40°45' |
| b | 35° | 35° | 34.5° | 33° | 34° | 34°18' |
34°30' |
| AB | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| MC | 58.7 | 61.4 | 55.4 | 58.5 | 60 | 58.9 | 59.3 |
| MM' | 15.7 | 18.6 | 13.3 | 15.7 | 17.8 | 16.2 | 16.2 |
| M'C | 43.0 | 42.8 | 42.1 | 42.8 | 42.2 | 42.6 | 43.1 |
In the seventh column the averages of the measure are worked out, and the eighth gives the calculated theoretical values. It will be noted that the values of a, b and MM' correspond very closely indeed, but that MC and M'C are very slightly less than they should be theoretically.
The very slight difference between the theoretical and the measured values is due to the introduction of a tiny facet, the culet, at the apex of the pavilions. This facet is introduced to avoid a sharp point which might cause a split or a breakage of the diamond.
What makes the agreement of these results even more remarkable is that in the manufacture of the diamond the polishers do not measure the angles, etc., by any instrument, but judge of their values entirely by the eye. And such is the skill they develop, that if the angles of two pavilions of a brilliant be measured, the difference between them will be inappreciable.
We may thus say that in the present-day well-cut brilliant, perfection is practically reached: the high-class is cut as near the theoretic values as is possible in practice, and gives a magnificent brilliancy to the diamond.
That some new shape will be evolved which will cause even greater fire and life than the brilliant is, of course, always possible, but it appears very doubtful, and it seems likely that the brilliant will be supreme for, at any rate, a long time yet.
